第二单元 用字母表示数
详细知识点,点击下面链接:
第三单元 三位数乘两位数
详细知识点,点击下面链接:
第四单元 多边形的认识
详细知识点,点击下面链接:
01 分数与小数的关系
分母是10的分数,可以化成一位小数;
分母是100的分数,可以化成两位小数;
分母是100的分数,可以化成三位小数;
……
分数转小数:
$\frac{6}{10}$ =0.6
$\frac{23}{100}$ = 0.23、$\frac{5}{100}$ = 0.05、$\frac{137}{100}$ = 1.37
$\frac{23}{1000}$ = 0.023、$\frac{5}{1000}$ = 0.005、$\frac{137}{1000}$ = 0.137
……
小数转分数:
0.23 = $\frac{23}{100}$ 、1.3 = $\frac{13}{10}$
02 小数点的移动
× 10 ,扩大10倍,小数点向右移动一位
× 100, 扩大100倍,小数点向右移动两位
× 1000, 扩大1000倍,小数点向右移动三位
0.2 × 10 = 2
0.3 × 100 = 30
2.53 × 1000 = 2530
÷ 10 ,缩小到原来的$\frac{1}{10}$,小数点向左移动一位
÷ 100 ,缩小到原来的$\frac{1}{100}$,小数点向左移动两位
÷ 1000 ,缩小到原来的$\frac{1}{1000}$,小数点向左移动三位
2 ÷ 10 = 0.2
3 ÷ 100 = 0.03
253 ÷ 1000 = 0.253
03 单位进率
长度单位:
- 米、分米、厘米、毫米【相邻两个单位之间的进率是10】
- 特殊:千米和米,1千米 = 1000米
1米 = 10分米、1分米 = 10厘米、1厘米 = 10毫米
1米=100厘米、1千米 = 1000米
重量单位:
- 吨、千克、克【相邻两个单位之间的进率是1000】
1吨 = 1000 千克、1千克 = 1000 克、
容量单位:
- 升、毫升【相邻两个单位之间的进率是1000】
1升 = 1000毫升
钱币单位:
- 元、角、分【相邻两个单位之间的进率是10】
1元 = 10角、1角 = 10分
1元 = 100分
单位转换:
- 大单位转小单位,是乘进率
- 例:3 米 = 3×10 = 30 分米
- 小单位转大单位,是除以进率
- 例:3 厘米 = 3÷10 = $\frac{3}{10}$ = 0.3 分米
- 复名数转单名数:
- 例:3 元 2 角 = 3 + 2 ÷ 10 = 3 + $\frac{2}{10}$ = 3 + 0.2 = 3.2 元
- 3 元 2 角 = 3 × 10 + 2 = 32 角
- 例:3 吨 25 千克 = 3 + 25 ÷ 1000 = 3 + $\frac{25}{1000}$ = 3+ 0.025 = 3.025 吨
- 3 吨 25 千克 = 3 × 1000 +25 =3025 千克
通常把量得的数和单位名称合起来叫做 名数;
只带有一个单位名称的,叫做 单名数;
带有两个或两个以上单位名称的叫做 复名数
04 分数与除法的关系
被除数 ÷ 除数 = $\frac{被除数}{除数}$
a ÷ b = $\frac{a}{b}$
3 ÷ 5 = $\frac{3}{5}$
12 ÷ 7 = $\frac{12}{7}$
05 分数的基本性质
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。这叫做 分数的基本性质。
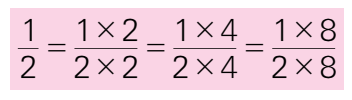
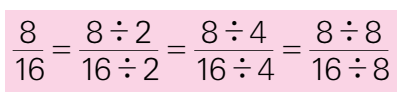
06 两位数乘11技巧
口诀:两边一拉、中间相加
例:25 × 11 = 272
解析:2 和 5 往两边拉开,中间填写 2 + 5 的和也就是 7,所以结果是 272
若中间两个数的和是两位数,则只留个位,正常往前进一
例:78 × 11 = 858
解析:7 和 8 往两边拉开,中间是 7 + 8 =15,中间写 5,而百位的 7 需要加进位 1,所以变成了8,结果就是858
07 2、3、5的倍数特征
2 的倍数特征:个位是0、2、4、6、8
5 的倍数特征:个位是 0 或 5
判断 2 和 5 的倍数时,看数的个位
3 的倍数特征:一个数的各位数之和时 3 的倍数,这个数就是 3 的倍数
例:234,因为 2 + 3 + 4 = 9,而 9 是 3 的倍数,所以 234 也是 3 的倍数
一个数是 2 的倍数,也可以说这个数含有因数 2
一个数是 3 的倍数,也可以说这个数含有因数 3
一个数是 5 的倍数,也可以说这个数含有因数 5
09 分数的意义
把 单位“1” 平均分 成若干份,表示这样的一份或几份的数,叫做分数
- 把一个整体平均分成几份,每份就是这个整体的几分之一
- 例如:把100个苹果平均分成 5 份,每份是这些苹果的 $\frac{1}{5}$
- 同一个整体,平均分成的分数不同,每一份所对应的物体个数也不同
- 例如:把100个苹果平均分成 5 份,每份是这些苹果的 $\frac{1}{5}$,每份含有100 ÷ 5 = 20 个苹果
- 例如:把100个苹果平均分成 10 份,每份是这些苹果的 $\frac{1}{10}$,每份含有100 ÷ 10 = 10 个苹果
拓展:这一类题,先看填空的后面是否有单位
- 无单位:是求 分率
- 方法:把单位”1”平均分成多少份,分母就是几;表示其中的几份,分子就是几
- 例:把100个苹果平均分成 5 份,每份是这些苹果的 $\frac{1}{5}$
- 解析:“的” 前是这些苹果,所以这100个苹果是单位“1”,平均分成了5份,分母就是5;每份指的是1份,表示这样的1份,分子就是 1,所以求出分率是 $\frac{1}{5}$
- 有单位:是求 具体数量
- 方法:单位“1”的总数 ÷ 平均分成的份数
- 例:把100个苹果平均分成 5 份,每份是 20 个苹果
- 解析:问多少个,有单位,是求具体数量,就用总数除以平均分的份数,列式为 100 ÷ 5 =20(个)
分率 和 具体数量
分数与原来学的整数、小数的最大区别:不仅可以表示具体数量,还可以表示分率
如何区分:看分数后面是否带单位
- 有单位的就是具体数量,例如 $\frac{1}{4}$ 米;
- 没单位的就是分率,例如 $\frac{1}{4}$;
10 单位 “1”
定义:一块月饼、一个图形、6面小旗、一条线段、一个计量单位……都可以看做一个整体,用自然数 1 来表示,通常把它叫做单位 “1”。
汇总:
- 把什么看做一个整体,其就是单位 “1”
- 把谁平均分就把谁看做一个整体,也就是单位 “1”
- 单位 “1” 用自然数 1 表示,也就是单位“1”的分率是 1
单位 “1” 和自然数 1 有什么区别?
自然数 1 只表示某一个具体事物,单位 “1” 既可以表示某一个具体事物,又可以表示一堆、一群或一些物体,即表示平均分的整体。
找单位 “1” 的方法
11 分数单位
$\frac{1}{9}$,$\frac{1}{5}$,$\frac{1}{2}$,$\frac{1}{13}$等都是分数单位
把单位“1”平均分成若干份,表示其中 1 份的数,叫做分数单位。
分数单位的分母与原分数的分母相同,分子是1。
- 例如:$\frac{3}{5}$ 的分数单位是 $\frac{1}{5}$
原分数的分子是几,就含有几个对应的份数单位
- 例如:$\frac{3}{5}$ 含有 3 个 $\frac{1}{5}$
13 用分数表示整体的一部分
通俗来说:求一个数是另一个数的几分之几?
整体就是我们说的单位“1”,首先找到单位“1”,然后用 部分的数量 ÷ 单位“1”的数量
例如:学校书法兴趣小组有17名同学,女同学有8名,女同学的人数占兴趣小组人数的几分之几?
- 首先判断,这个问题中“的”字前面是【兴趣小组】,所以单位“1”是兴趣小组
- 部分指的是女同学,所以列式为:女生人数 ÷ 兴趣小组的人数 = $\frac{女生人数}{兴趣小组的人数}$
- 8 ÷ 17 =$\frac{8}{17}$
学校书法兴趣小组有17名同学,女同学有8名,男同学的人数占兴趣小组人数的几分之几?
男同学:17 - 8 = 9(名)
9 ÷ 17 = $\frac{9}{17}$
答:男同学的人数占兴趣小组人数的 $\frac{9}{17}$